বৃত্ত কাকে বলে, বৃত্তের বৈশিষ্ট্য, কেন্দ্র, ব্যাস, পরিধি

আমরা জানতে পারবো বৃত্ত কাকে বলে, বৃত্ত কি, বৃত্তের কেন্দ্র, ব্যাস, ব্যাসার্ধ, ক্ষেত্রফল, পরিধি এবং বৃত্তের সমীকরণ সম্পর্কে……

বৃত্ত কাকে বলে (britto kake bole)

একটি নির্দিষ্ট  বিন্দুকে কেন্দ্র করে সমান দূরত্ব বজায় যে বক্ররেখা একবার ঘুরে ঐ বিন্দুতে আসে তাকে বৃত্ত বলে।  অন্যভাবে বলা যায, একটি নির্দিষ্ট বিন্দুকে কেন্দ্র করে সর্বদা সমন দূরত্ব বজায় রেখে অন্য একটি বিন্দু তার চারদিকে একবার ঘুরে ওই বিন্দুতে মিলিত হয় এবং যে ক্ষেত্র তৈরি করে বা উৎপন্ন করে তাকে বলে বৃত্ত বলে।

বৃত্তের বৈশিষ্ট্য

• বৃত্তের কেন্দ্র বিন্দু থেকে যেকোনো বিন্দুর দূরত্ব হলো ব্যাসার্ধ।
• বৃত্তের কেন্দ্র বিন্দু থেকে বৃত্তের যেকোনো দুটি বিন্দুর দূরত্ব সমান।
• বৃত্তের যেকোনো দুটি বিন্দুর মধ্য দিয়ে একটি সরল রেখাংশ টানা যায়। এই সরল রেখাংশকে বৃত্তের ব্যাস বলা হয়।
• বৃত্তের যেকোনো ব্যাস বৃত্তকে দুটি সমান অংশে ভাগ করে।
• বৃত্তের যেকোনো ব্যাসের মধ্যবিন্দু বৃত্তের কেন্দ্র।
• বৃত্তের যেকোনো দুটি ব্যাসের মধ্যবিন্দু পরস্পর যুক্ত হয়ে বৃত্তের একটি ব্যাস গঠন করে।
• বৃত্তের যেকোনো বিন্দু থেকে বৃত্তের কেন্দ্র বিন্দু এবং বৃত্তের স্পর্শবিন্দু দ্বারা গঠিত ত্রিভুজ একটি সমকোণী ত্রিভুজ।

বৃত্তের কেন্দ্র কি

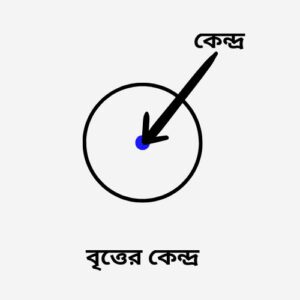
বৃত্ত এর কেন্দ্র হল এমন একটি নির্দিষ্ট বিন্দু যে বিন্দু থেকে পরিধির ওপর অবস্থিত সকল বিন্দুর দূরত্ব সমান তবে ওই নির্দিষ্ট বিন্দুতে বৃত্তের কেন্দ্র বলে। একটি বৃত্তে কেবলমাত্র একটি নির্দিষ্ট কেন্দ্র থাকে। একটি বৃত্তের একাধিক কেন্দ্র হতে পারে না, কিন্তু একটি কেন্দ্রের একাধিক বৃত্ত হতে পারে না।

বৃত্তের  জ্যা

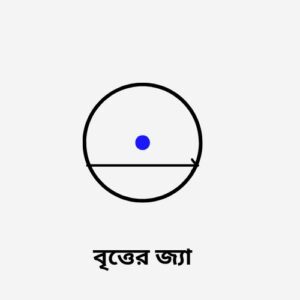
একটি বৃত্তের পরিধির উপর অবস্থিত যেকোন দুটি বিন্দুর সংযোগ রেখাংশকে জ্যা বলে। একটি বৃত্তে একাধিক জ্যা থাকতে পারে। বৃত্তের  ব্যাসই হল সবচেয়ে বৃহত্তর জ্যা। সমান সমান  জ্যা কেন্দ্র থেকে  সমান দূরত্বে অবস্থিত। বৃত্তের যেকোন জ্যা এর মধ্যবিন্দুতে লম্ব অংকন করলে সেটি কেন্দ্রগামী হবে।

বৃত্তের ব্যাস

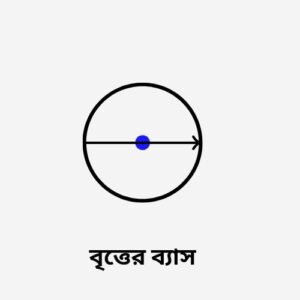
একটি বৃত্তের পরিধির উপর অবস্থিত যেকোন দুটি বিন্দুর সংযোগ রেখাংশকে জ্যা বলে এবং জ্যা যদি কেন্দ্রগামী হয় তাহলে ওই জ্যা কে বৃত্তের ব্যাস বলে।  একটি বৃত্তে একাধিক বৃত্তের  ব্যাস থাকতে পারে। ব্যাস হল ব্যাসার্ধের  দ্বিগুণ।  একটি বৃত্তের ব্যাসের মধ্যবিন্দু  হলো সেই বৃত্তের কেন্দ্র।  একে  D দ্বারা প্রকাশ করা হয়.

বৃত্তের ব্যাস= 2 x বৃত্তের ব্যাসার্ধ

অথবা, D= 2 x R

বৃত্তের ব্যাসার্ধ

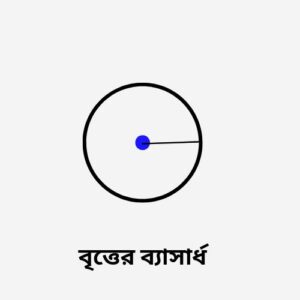
একটি বৃত্তের পরিধি থেকে  কেন্দ্র পর্যন্ত দূরত্বকে  ব্যাসার্ধ বলে। বৃত্তের ব্যাসার্ধ হলো ব্যাসের অর্ধেক।

বৃত্তের ব্যাসার্ধ = বৃত্তের ব্যাস / 2

অথবা, R = D / 2

বৃত্তের পরিধি

একটি বৃত্তের কেন্দ্র থেকে সমান দূরত্ব বজায় রেখে কোন বিন্দু যে পথে চলে সেই পথকে পরিধি বলে। বৃত্তের পরিধি বলতে বৃত্তের পরিসীমকে বুঝায়।

বৃত্তের পরিধি বের করার সূত্রঃ  পরিধি = 2πr

এখানে,π = 3.1416 ।  r = বৃত্তের ব্যাসার্ধ

বৃত্তের চাপ

বৃত্তের পরিধির যেকোন অংশকে বৃত্তচাপ বলে। একটি বৃত্তে দুইটি চাপ থাকে। যার একটি উপচাপ আর অন্যটি অধিচাপ। বৃত্তের ছোট চাপটিকে উপচাপ আর বড় চাপটিকে  অধিচাপ বলে অর্থাৎ বৃত্তের বৃহত্তম চাপ হলো অধিচাপ।

বৃত্ত চাপের দৈর্ঘ্য নির্ণয়ের সূত্র s = πrθ/180°

 – এখানে, π= 3.1416

R = বৃত্তের ব্যাসার্ধ

Θ = কোন

বৃত্তের ক্ষেত্রফল

বৃত্তের ক্ষেত্রফল নির্ণয়ের সূত্র = πr²

এখানে, π= 3.1416, R = বৃত্তের ব্যাসার্ধ

বৃত্তের সমীকরণ

যদি একটি বৃত্তের কেন্দ্র (a,b) এবং ব্যাসার্ধ r হয়। তবে,

বৃত্তের সমীকরণ হবে (x-a)² + (y-b)² = r²

বৃত্তের সমীকরণের সাধারণ রূপ
একটি বৃত্তের সাধারণ সমীকরণ হলঃ x² + y² + 2gx + 2fy + c = 0

এখানে,

(x, y) হল বৃত্তের উপরের যেকোনো বিন্দুর স্থানাঙ্ক।
g, f, এবং c হল ধ্রুবক।
বৃত্তের কেন্দ্র ও ব্যাসার্ধ নির্ণয়

কেন্দ্রঃ (-g, -f)
ব্যাসার্ধঃ √(g² + f² – c)

বিভিন্ন ধরনের বৃত্তের সমীকরণ

• মূলবিন্দুতে কেন্দ্রবিশিষ্ট বৃত্ত: x² + y² = r²
• যদি একটি বৃত্তের কেন্দ্র (a,b) এবং ব্যাসার্ধ r হয়। বৃত্তের সমীকরণ হবে (x-a)² + (y-b)² = r²

উদাহরণ
১)  x² + y² – 4x + 6y – 3 = 0 এই সমীকরণটি কোন বৃত্তের প্রতিনিধিত্ব করে। এই বৃত্তের কেন্দ্র ও ব্যাসার্ধ নির্ণয় করো।

সমাধান: এখানে, g = -2, f = 3, এবং c = -3. ∴ কেন্দ্র = (-g, -f) = (2, -3) ∴ ব্যাসার্ধ = √(g² + f² – c) = √((-2)² + 3² – (-3)) = √16 = 4

সুতরাং, দেওয়া সমীকরণটি একটি বৃত্তের প্রতিনিধিত্ব করে যার কেন্দ্র (2, -3) এবং ব্যাসার্ধ 4 একক।

২) যদি একটি বৃত্তের কেন্দ্র (১,২) এবং ২ ব্যাসার্ধ বিশিষ্ট বৃত্তের সমীকরণ নির্ণয় কর?

সমাধানঃ  কেন্দ্র (১,২) এবং দুই ব্যাসার্ধ বিশিষ্ট বৃত্তের সমীকরণ হবে  (x-১)² + (y-২)² = ২²